该公告已过公示时间，对该公告内容进行下架处理，给您带来的不便敬请谅解。

【试题练习】

一个山丘的形状如下图所示。甲、乙两人同时从A点出发匀速前往B点，到达B点后立刻返回。甲上坡速度为3米/秒，下坡速度为5米/秒；乙上坡速度为2米/秒，下坡速度为3米/秒。问两人首次相遇时，距A点的路程为多少米？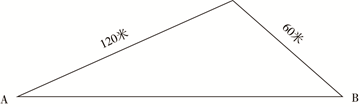

A.108

B.138

C.150

D.162

正确答案：B

【解析】第一步，本题考查行程问题。
第二步，计算甲从A到B的时间为120÷3＋60÷5＝52（秒），乙从A到B的时间为120÷2＋60÷3＝80（秒）。这就说明当甲到达B地时乙还在上坡路段行驶，当时间为60秒时，乙到达坡顶，这时甲已开始往回走，甲回程上坡走完3×（60－52）＝24（米）时，乙刚好开始下坡，这时甲乙相距60－24＝36（米），接着甲乙会首次相遇。
第三步，根据相遇公式，36＝（3＋3）×t，解t＝6（秒），那么可以计算出乙从坡顶行走的距离为3×6＝18（米），这时乙行走的总路程就是两人首次相遇时距离A点的路程，为120＋18＝138（米）。
因此，选择B选项。