1、某技校在每月首日招收学员,学习时限以月为周期,每月首日为考核日,考核通过即离校。每批学员学习1个月后,在次月初考核通过的比例为10%,而学习2个月后,仍未通过考核的占该批学员的50%,学习3个月后该批学员全部考核通过离校。如果从3月份起,该技校开始招收学员且每个月招收300名学员,则同年7月2日在该技校的学员有多少名?
A.540
B.600
C.720
D.810
2、现有5盒动画卡片,各盒卡片张数分别为:7、9、11、14、17。卡片按图案分为米老鼠、葫芦娃、喜洋洋、灰太狼4种,每个盒内装的是同图案的卡片。已知米老鼠图案的卡片只有一盒,而喜洋洋、灰太狼图案的卡片数之和比葫芦娃图案的多1倍,那么图案为米老鼠的卡片的张数为?
A.7
B.9
C.14
D.17
3、A、B两地各有一批相同数量的货物箱需由某运输队用卡车完成交换,假设每辆卡车运送的货物箱数量相同,运输队首先从A地出发,中途10辆卡车因抛锚彻底退出这次运输,使得其余车辆必须每车再多运2箱,到达B地卸货后又有15辆卡车不返程,参与返程的卡车每辆都需比出发时多装运6箱。那么两地共有货物多少箱?
A.2000
B.1800
C.3600
D.4000
4、在一次马拉松比赛中,某国运动员包揽了前四名,他们佩戴的参赛号码很有趣:运动员甲的号码加4,乙的号码减4,丙的号码乘4,丁的号码除以8,所得的数字都一样。这四个号码中有1个三位数号码,2个两位数号码,1个一位数号码,且其中一位运动员在比赛中取得的名次也与自己的号码相同。那么其中三位数的号码为:
A.120
B.128
C.256
D.512
5、小张需租某店铺制作贩售绿茶。他计划以8万元现金及若干固定袋数的绿茶作为一年租金。若每袋茶叶售价75元,则一年租金等价于每平方米70元;若每袋茶叶在原价的基础上再涨价三分之一,则一年租金相当于每平方米80元。那么该店铺的面积为多少平方米?
A.1600
B.2000
C.2500
D.3000
63、某饮料厂生产的A、B两种饮料均需加入某添加剂,A饮料每瓶需加该添加剂4克,B饮料每瓶需加3克。已知370克该添加剂恰好生产了两种饮料共计100瓶,则A、B两种饮料各生产了多少瓶?
A.30、70
B.40、60
C.50、50
D.70、30
【请点击下一页查看答案与解析】
1、
【答案】C
【正确率】50%
【三级知识点】数量关系-数学运算-基础应用题
【解析】
第一步,本题考查基础应用题,用枚举法解题。
第二步,根据题目描述,列出下表:
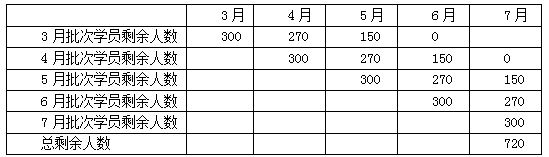
同年7月2日该技校学员的总数,包括5月批次学员剩余150名,6月批次学员剩余学员270名,7月批次学员剩余学员300名,那么共有学生150+270+300=720(名)。
因此,选择C选项。
2、
【答案】A
【正确率】33%
【三级知识点】数量关系-数学运算-基础计算问题
【解析】
第一步, 本题考查基础计算问题,用数字特性法解题。
第二步, 5盒动画卡片共有7+9+11+14+17=58(张),喜洋洋、灰太狼图案的卡片之和比葫芦娃图案多1倍,即是葫芦娃图案的2倍。那么喜洋洋+灰太狼+葫芦娃=3×葫芦娃,即喜洋洋+灰太狼+葫芦娃的卡片数是3的倍数,喜洋洋+灰太狼+葫芦娃的卡片数=总数-米老鼠的卡片数,那么总数-米老鼠的卡片数是3的倍数。
第三步, 代入选项验证,A选项,58-7=51,是3的倍数;B选项,58-9=49,不是3的倍数,排除;C选项,58-14=44,不是3的倍数,排除;D选项,58-11=47,不是3的倍数,排除。只有A选项满足题意。
因此,选择A选项。
3、
【答案】C
【正确率】48%
【三级知识点】数量关系-数学运算-基础应用题
【解析】
第一步,本题考查基础应用题,用方程法解题。
第二步,设原有卡车数量x,每辆卡车货物数量y;10辆卡车退出后,卡车数量(x-10)辆,每辆卡车货物数量为(y+2);同理,返程时卡车数量(x-10-15),每辆卡车货物数量(y+6)。因此可列出等式xy=(x-10)×(y+2)=(x-10-15)×(y+6)。
第三步,整理可得2x-10y=20①,6x-25y=150②,联立解得x=100,y=18。则每地货物量为1800箱,AB两地共有3600箱。
因此,选择C选项。
4、
【答案】B
【正确率】56%
【三级知识点】数量关系-数学运算-约数倍数问题
【解析】
第一步,本题考查约数倍数问题,用代入排除法解题。
第二步,因未知数较多,设中间变量,一样的数字为4n。则甲乙丙丁分别为:4n-4,4n+4,n,32n,比较可得三位数号码为32n。而n≤4,可得32n≤128。
第三步,三位数不超过128且是32的倍数,排除A、C、D。
因此,选择B选项。
5、
【答案】D
【正确率】65%
【三级知识点】数量关系-数学运算-基础应用题
【解析】
解法一:
第一步, 本题考查基础应用题,用方程法解题。
第二步, 设A种饮料生产了x瓶,则B种饮料生产了(100-x)瓶,根据370克添加剂恰好用完,可列方程:4x+3×(100-x)=370,解得x=70,即生产70瓶A种饮料,那么生产B种饮料100-70=30(瓶)。
因此,选择D选项。
解法二:
第一步,本题考查基础应用题,用假设法解题。
第二步,假设都生产A饮料,则需要添加剂100×4=400(克),但实际只有370克添加剂,超出400-370=30(克),每生产1瓶B饮料可比生产1瓶A饮料少用4-3=1(克)添加剂,那么生产B饮料30/1=30(瓶),则生产A饮料100-30=70(瓶)。
因此,选择D选项。










