概率问题一直是每年公务员招录多省联考行政职业能力测试中的一类重点题型,尤其是在2020年和2021年概率问题题量占比相对于前几年明显增加,而且题型上也出现了一些新的变化,比如在2020年和2021年连续两年都考查了几何概率的问题。因此对于准备参加公务员招录多省联考的考生,应该在复习中将几何概率问题作为重点复习内容之一。今天我们就结合最近两年的概率问题的题型变化,给大家分享一下关于几何概率问题的求解方法。
几何概率有两个重要特征,无限性和等可能性。即针对概率问题采用随机试验的方法测定概率,试验的结果有无限可能,每一种可能出现的概率是相同的。比如:我们向一个边长为1米的正方形区域投掷石块,石块落点位置有无数多种情况;因为是随机投掷,石块落在任意一点的概率是相等的。又比如,我们早上8:00~9:00到单位,这期间我们可能任意一个时刻到达单位,这些时刻有无数多种情况,我们任意时刻到达的概率是相等的。
类似上面的例子,我都可以将事件投射在几何图形中,按几何概率思路进行计算。
比如:例1(2019-黑龙江-72)某公司职员预约某快递员上午9点30分到10点在公司大楼前取件,假设两人均在这段时间内到达,且在这段时间到达的概率相等。约定先到者等后到者10分钟,过时交易取消。快递员取件成功的概率为:

在求解时,我们可以将题目描述时间的每一种情况投射成几何图形中的某一点,比如根据题目描述的时间范围做如下图示。

图中横坐标表示公司职员(发件人)到达大楼前的时间,纵坐标表示快递员到达大楼前的时间。下面我们将问题分成几个特殊时间节点进行分析:(根据题意,讨论时间范围限定在9:30~10:00这半小时内)
第一种情况,发件人9:30分到达,则快递员在9:30~9:40之间到达,可以取件成功。在图示表示为线段A1B1。
第二种情况,发件人9:40分到达,则快递员在9:30~9:50之间到达,可以取件成功。在图示表示为线段A2B2。
第三种情况,发件人9:50分到达,则快递员在9:40~10:00之间到达,可以取件成功。在图示表示为线段A3B3。
第四种情况,发件人10:00分到达,则快递员在9:50~10:00之间到达,可以取件成功。在图示表示为线段A4B4。
因此,将例1描述的情况,投射到几何坐标中,由A1A2A3A4B4B3B2B1围成的多边形区域内的任意一个点都表示取件成功;将A1MB4N四点连接,得到快递员与职员随机到达大楼前的情况。如下图所示:
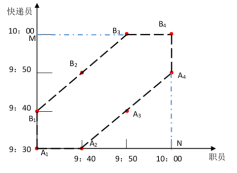
所以,能够成功取件的概率为A1A2A3A4B4B3B2B1围成的多边形区域面积占A1MB4N四点连接区域的面积比例。直接计算过程比较繁琐,考虑反向求解,设A1N=A1M长度为3,则三角形B1MB3面积为2,三角形A2NA4面积为2,四边形A1MB4N面积为9,A1A2A3A4B4B3B2B1围成的多边形区域面积为9-2-2=5,所以成功取件的概率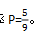
因此,例1选择C选项。
通过这样一个例题详细解释,希望大家能够掌握几何概率问题求解的基本思路。
几何概率有两个重要特征,无限性和等可能性。即针对概率问题采用随机试验的方法测定概率,试验的结果有无限可能,每一种可能出现的概率是相同的。比如:我们向一个边长为1米的正方形区域投掷石块,石块落点位置有无数多种情况;因为是随机投掷,石块落在任意一点的概率是相等的。又比如,我们早上8:00~9:00到单位,这期间我们可能任意一个时刻到达单位,这些时刻有无数多种情况,我们任意时刻到达的概率是相等的。
类似上面的例子,我都可以将事件投射在几何图形中,按几何概率思路进行计算。
比如:例1(2019-黑龙江-72)某公司职员预约某快递员上午9点30分到10点在公司大楼前取件,假设两人均在这段时间内到达,且在这段时间到达的概率相等。约定先到者等后到者10分钟,过时交易取消。快递员取件成功的概率为:

在求解时,我们可以将题目描述时间的每一种情况投射成几何图形中的某一点,比如根据题目描述的时间范围做如下图示。

图中横坐标表示公司职员(发件人)到达大楼前的时间,纵坐标表示快递员到达大楼前的时间。下面我们将问题分成几个特殊时间节点进行分析:(根据题意,讨论时间范围限定在9:30~10:00这半小时内)
第一种情况,发件人9:30分到达,则快递员在9:30~9:40之间到达,可以取件成功。在图示表示为线段A1B1。
第二种情况,发件人9:40分到达,则快递员在9:30~9:50之间到达,可以取件成功。在图示表示为线段A2B2。
第三种情况,发件人9:50分到达,则快递员在9:40~10:00之间到达,可以取件成功。在图示表示为线段A3B3。
第四种情况,发件人10:00分到达,则快递员在9:50~10:00之间到达,可以取件成功。在图示表示为线段A4B4。
因此,将例1描述的情况,投射到几何坐标中,由A1A2A3A4B4B3B2B1围成的多边形区域内的任意一个点都表示取件成功;将A1MB4N四点连接,得到快递员与职员随机到达大楼前的情况。如下图所示:

所以,能够成功取件的概率为A1A2A3A4B4B3B2B1围成的多边形区域面积占A1MB4N四点连接区域的面积比例。直接计算过程比较繁琐,考虑反向求解,设A1N=A1M长度为3,则三角形B1MB3面积为2,三角形A2NA4面积为2,四边形A1MB4N面积为9,A1A2A3A4B4B3B2B1围成的多边形区域面积为9-2-2=5,所以成功取件的概率
因此,例1选择C选项。
通过这样一个例题详细解释,希望大家能够掌握几何概率问题求解的基本思路。










