在行测数量关系模块的试题中,大家经常遇到排列组合问题,而且排列组合一直是考核重点,因为涉及情况复杂,题型多样,因此,排列组合同时也成为了我们在行测备考路上的绊脚石。行测考核中出现的排列组合问题中,不仅仅涉及到相邻不相邻的排列问题,还涉及到直线和环形排列问题,还有隔板法和错位排列的应用,都是我们在备考时需要关注的重点。除此以外,还有一类排列组合题型,往往容易被大家所忽略,一旦遇到,可能会让我们抓耳挠腮,那就是平均分组问题。今天我们就来重点讨论这个问题。
【例1】某班共有8名战士,现在从中挑出4人平均分成两个战斗小组分别参加射击和格斗考核,问共有多少种不同的方案?
A. 210
B. 420
C. 630
D. 840
![]()
【答案】B。华图解析:这是一道排列组合中关于平均分组的问题。根据题干要求,平均分成两个战斗小组的4个人,是从8人中选出的,所以先进行选人,8选4,与顺序无关,所以是。接着从选出的4人中,再选出两人放在射击小组,是,最后从剩余两人中选两人加入格斗小组,很显然,如果表示出来就是,不写也可以,因为只剩下两人了,只有这唯一的一种选法,压根不需要选,这两个人直接就到格斗小组去了。以上几个做法属于分步,故使用乘法,所以最终不同的方案是(种)。所以,本题选择B选项。
【例2】某班共有8名战士,现在从中挑出4人平均分成两个战斗小组,问共有多少种不同的方案?
A. 210
B. 420
C. 630
D. 840
![]()
【答案】A。华图解析:本题也属于排列组合中平均分组的问题,但和例1中不同的是,挑出来的4人,分成的两个战斗小组没有区别,既没有分出1组和2组,也没说分出射击组和格斗组等其他两个不同的组。这样一来,我们再按照例1中的做法恐怕就有问题了吧。具体我们来分析。首先仍是从8人中选4人,是。为了让大家理解的更清晰和透彻,这里我们假设从8人中选出4人的其中一次选出的是甲、乙、丙、丁四个人,接着我们从选出的甲、乙、丙、丁中选两人放在其中一组,是,假定这时选出的两人是甲、乙两人,那么另外丙、丁两人自然就分在另外一组了,所以我们写成。聪明的你,发现这里面的问题了没?我们不妨再假设一次,这次我们假设从甲、乙、丙、丁四个人中先选出的两个人不是甲、乙两人,而是丙、丁两人,那么剩余甲、乙两人自然就到另外一组去了。由于两个组,并没有任何区别,而我们若还像例1中写成,就是默认这两个组是有区别的了,所以本题我们再这样做肯定是有问题的。是考虑到了两组的排序的,相当于里面多乘了两个元素的排序,即,故最终方案数需要在基础上除掉两个元素的排序,即(种),因此,本题选择A选项。
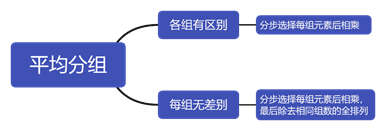
通过以上两道真题解答过程的详细呈现,相信大家不难总结出,在平均分组时,若小组各不相同,则无需最后除去之前步骤中的排序的数量;若是各小组没有任何差别,则需要在之前的步骤中除去多余的排序数量。相信通过本篇总结,一定可以帮助大家快速且正确地解答此类题目。