该公告已过公示时间，对该公告内容进行下架处理，给您带来的不便敬请谅解。
扫码领取资料,了解更多
【试题练习】
如图，在面积为300的梯形ABCD中，下底边BC为上底边AD的2倍，E、F分别为CD、BC的中点，连接AE、AF与BD分别相交于M、N两点，则三角形AMN的面积为：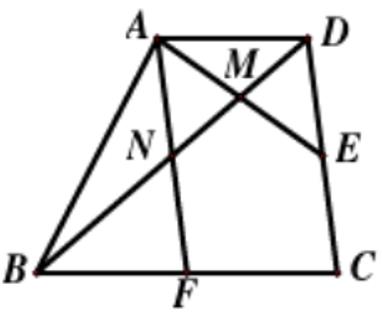
A.25
B.23
C.20
D.15
正确答案：A
【解析】第一步，本题考查几何问题。
第二步，由于BC＝2AD，且F是中点，故AD＝BF，故三角形AND与三角形FNB全等，则BN＝DN，故N为AF的中点，也是BD的中点，分析可知三角形BNF的面积为梯形的
，即
,所以三角形AND的面积也为50。在四边形AFCD中，
，AD=FC，所以四边形AFCD为平行四边形，AF=CD，N、E为AF和CD的中点，所以AN=DE，三角形ANM和三角形EDM的面积也相等，则可知M为ND中点，所以三角形ANM的面积为三角形AND的一半，则三角形AMN的面积为
。
因此，选择A选项。
