2022年省考行测数量关系概率问题简单研究
想必大家都有过“彩票双色球,中奖500万”的梦想,但结果是,极少有人能实现,这是为什么呢?因为中奖的号码只有一个,而非中奖的号码太多了,大约上千万种,所以一等奖的中奖概率太低了。那么概率是如何计算的呢,我们一起来研究一下。

在行测考试中,概率问题就是很重要的一个考点。首先,我们要知道什么是概率以及他的基本公式。概率:某件事情发生的可能性。基本公式:
但是,在行测的考试中,满足条件的情况和总的情况数都是需要我们计算的,而且,情况数的计算往往需要用到排列组合的相关知识,最后,计算概率的时候也需要用到加法和乘法两种原理,在概率中,我们可以概括为分类概率和分步概率。
分类概率:某件事情可以在多种情况下完成,每种情况之间没有影响,那么,要先计算每种情况发生的概率,然后把每种情况的概率相加就是这件事情发生的概率。
分步概率:某件事情需要通过多个步骤才能完成,每个步骤缺一不可,那么,要先计算每个步骤发生的概率,然后把每个步骤的概率相乘就是这件事情发生的概率。
有了相关的基础知识储备,我们就可以解决部分问题了。我们通过一道题应用一下。
【例】某单位的一个科室从10名职工中随机挑选2人去听报告,要求女职工人数不得少于1人。已知该科室女职工比男职工多2人,小张和小刘都是该科室的女性职工,则她们同时被选上的概率在以下哪个范围内?
A.3%到5%B.小于2%
C.2%到3%D.大于5%
【解析】首先,科室一共10人,女职工比男职工多2人,可知女职工有6人,男职工有4人。选择2个人,满足条件的情况就是小张和小刘都被选上,即满足条件的情况数是1;总情况数则需要分类讨论:6个女职工选择2人,有15种方法;10人中选1男1女,有24种方法,一共39种方法,约等于2.6%。因此,选择C选项。

通过这道题我们可以看出,概率问题的经常将考点设置在满足条件的情况数和总的情况数上,穿插排列组合的相关考点。另一个重点在于分析:分步进行,计算每步的概率,使用乘法原理;分类讨论,计算每种情况的概率,应用加法原理。此外,再给大家介绍一种方法:当我们通过分析发现正向考虑情况数太多时,可以考虑求反向的情况数,先计算反向概率,然后用“1-反向概率”得出最终答案。
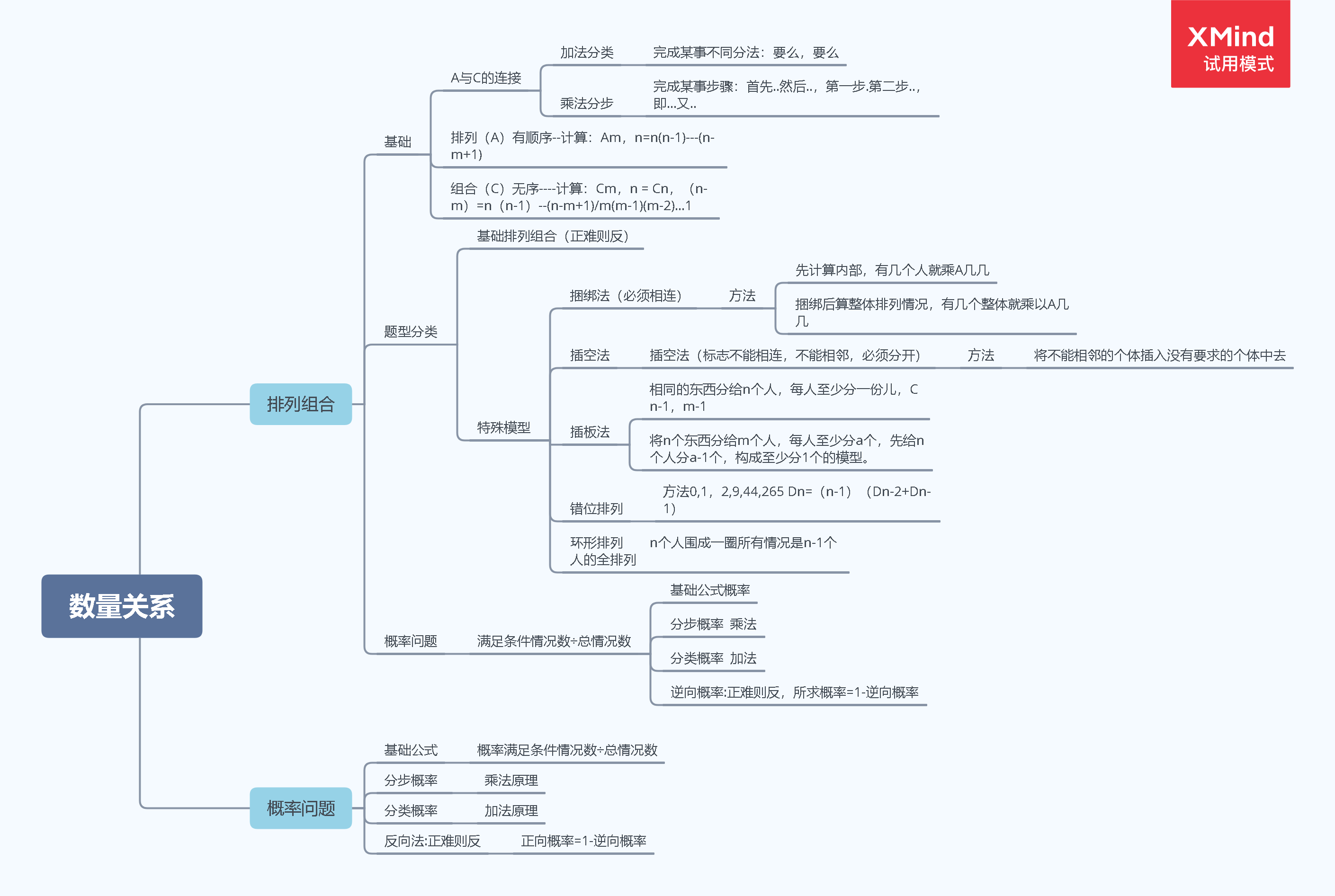
关于概率问题,首先要掌握基本公式,有明确的求解方向,然后还需要一些排列组合的基础,因为在计算情况数时往往涉及到相关计算,最后分析是概率类型,进行计算。总之,学好排列组合,概率问题一定不是问题。
今天的知识点就介绍到这,希望可以帮助大家,如果还有什么不清楚的,可以前来咨询,会有相关专业的老师帮助大家解决问题。大家加油,祝大家早日上岸!










