2022年行测数量关系:两题讲透不定方程(组)的解法
近些年不定方程(组)的求解在国联考中频繁出现,实际上它有两种考法,但很多同学并不能准确区分,以至于在遇到不定方程(组)求解时会很蒙圈。下面这两题你们能准确区分吗?第一题:M小区停车收费,小型车辆每天5元,中型车辆每天8元,大型车辆每天10元。某天小区总共停了20辆车,共收费153元,那么当天大型车辆可能有多少辆?A.8B.9C.10D.11。第二题:若买6个订书机、4个计算器和6个文件夹共需504元,买3个订书机、1个计算器和3个文件夹共需207元,则购买订书机、计算器和文件夹各5个所需的费用是多少元?A.465元B.475元C.485元D.495元 
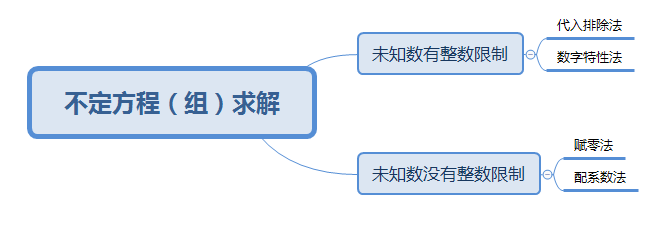
从表面来看,如果用方程去做的话,两个题都是不定方程组,那它们的求解方法是一样的吗?或者大家去思考下,这两个方程组有什么本质区别?细心的同学可能发现了,第一个题目中未知数指的是车的数量,第二个题目中未知数指的是价格,区别在于第一个题目中未知数必须是整数,而第二个题目中未知数可以不是整数,明白这一点,下面的分类就很好理解了。
(一)未知数有整数限制
当方程(组)中未知数有整数限制时,这种方程(组)的解是有限多个的,可以采用代入法或者一些数字特性去进行求解。以第一题为例,可设小车、中车和大车的数量分别为x,y,z,可得方程组为false,简单消元可得false,结合选项代入容易验证当z=10时,y=1满足题意。因此选择C选项。
(二)未知数没有整数限制
当方程(组)中未知数没有整数限制时,这种方程(组)的解是无穷多个的,针对这种方程组可以采用赋零法和配系数法进行求解。下面对这两种方法进行讲解,先讲第一种赋零法。设订书机、计算器和文件夹的单价分别为x,y,z,可得方程组为false,由于单价可以为非整数,所以这个方程组有无穷多个解,但题目求的是5(x+y+z),说明x+y+z是一个定值,因此任意找一组特解代入5(x+y+z)即可求出答案。为了计算简便,可令某一个未知数为0进行求解,这就是赋零法的由来。不妨令x=0,解得y=45,z=54,因此5(x+y+z)=495。再讲第二种方法配系数法,这个方法就是将这两个方程进行线性组合就可以求出目标式,观察这个方程组,将两式相减,的3(x+y+z)=297,所以5(x+y+z)=297÷3×5=495。需要说明的是,第二类不定方程组的两种解法各有优劣,第一种方法过程稍显麻烦,但操作简单,可以进行套路化操作,第二种方法过程简单,但需要一定的观察能力和数字敏感性,大家在考场上可以灵活处理。
通过以上两个例子,相信大家对不定方程(组)这个考点已经有了更深的了解。更多相关考试信息请及时关注华图教育官网!