一、方程问题的考情
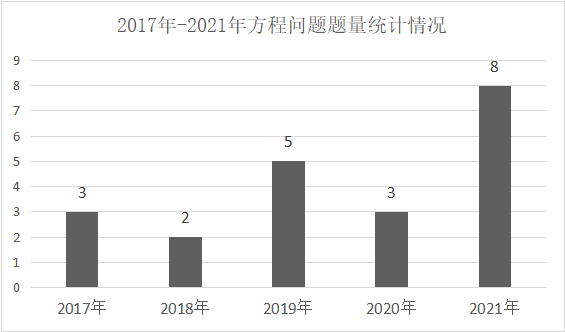
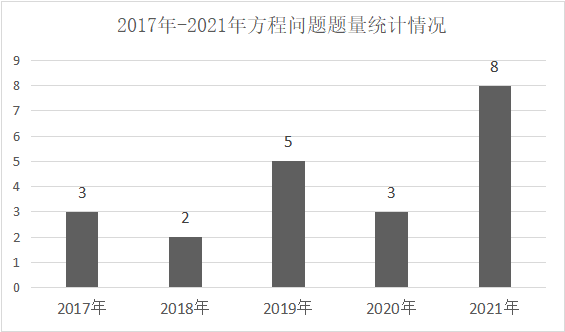
方程问题在国考中占据非常重要的地位,为何得出此结论呢?因为方程问题在考题中每年必考且题量不少于1题,大家请看近5年国考副省级考题中方程问题的题量统计图。
方程问题考的多,那么难度如何呢?接下来给大家展示近5年难易程度情况表
| 国考副省级 | |||||
| 2017年 | 2018年 | 2019年 | 2020年 | 2021年 | |
| 难 | 1 | 2 | |||
| 中 | 3 | 1 | 3 | 1 | 8 |
| 易 | 2 | ||||
通过这张表,我们可以了解到方程问题的难度集中在中等难度,解方程的方法除了常规的解法,比如移项相消,加减消元法,代入消元法外,今天再给各位同学分享3种解方程的方法。

二、真题感知
解法1:奇偶特性法。
【例1】每年三月某单位都要组织员工去A、B两地参加植树活动。已知去A地每人往返车费20元,人均植树5棵,去B地每人往返车费30元,人均植树3棵,设到A地员工有x人,A、B两地共植树y棵,y与x之间满足y=8x-15,若往返车费总和不超过3000元,那么,最多可植树多少棵?
A.489
B.400
C.498
D.500
【答案】A
【解析】方法一:因为A地有x人,所以A地总车费是20x,A地植树总棵数是5x。因为A、B两地总棵数是y棵,所以B地植树总棵数是y-5x=8x-15-5x=3x-15,那么B地员工人数是(3x-15)3=(x-5)人,B地总车费是30(x-5),两地总车费不超过3000元,最大就是3000元,则列方程20x+30(x-5)=3000,解方程x=63,最后y=863-15=489,因此,选择A选项。
方法二:题目最终求y值,8x是偶数,15是奇数,偶数减奇数等于奇数,所以y值是奇数,因此,选择A选项。
解法2:倍数特性法。
【例2】某地调派96人分赴车站、机场、超市和学校四个人流密集的区域进行卫生安全检查,其中 公共卫生专业人员有62人。已知派往机场的人员是四个区域中最多的,派往车站和超市的人员中,专业人员分别占64%和65%,派往学校的人员中,非专业人员比专业人员少30%,问派往机场的人员中,专业人员的占比在四个区域中排名:
A第1
B第2
C第3
D第4
【答案】A
![]()
【解析】假设车站,机场,超市,学校的人数分别是a、b、c、d,则可以列方程a+b+c+d=96,接下来无法再找到等量关系,所以方程法不容易得出结果,因此我们考虑倍数特性法辅助求解方程。车站的专业人员与派往车站的总人数比是,超市的专业人员与派往超市的总人数比是,因为派往学校的人员中,非专业人员比专业人员少30%,所以学校的专业人员比重是,因为总人数是96人,所以车站,超市,学校的人数只能分别是25人、20人、17人,那么三个地方的专业人员只能分别是16人、13人、10人,则派往机场的总人数是96-25-20-17=34人,机场的专业人员是62-16-13-10=23人,机场的专业人员比重是2334=67.6%,比重最大。因此,选择A选项。
解法3:代入法
【例3】如图所示,在长为64米、宽为40米的长方形耕地上修建宽度相同的两条道路(一条横向、一条纵向),把耕地分为大小不等的四块耕地。已知,修路后耕地总面积为1377平方米,则该道路路面宽度为多少米?
A 10
B 11
C 12
D 13
【答案】D
【解析】假设道路路面宽度是x米,列方程(64-x)(40-x)=1377,因为此方程是一元二次方程,不容易求解,所以考虑代入验证,代入D.13验证,则(64-13)(40-13)=1377,符合等量关系,因此,选择D选项。
怎么样,小伙伴们,学会了吗?让我们赶紧做几个题练习练习吧。
【练习1】甲、乙两个单位周末分别安排60%和75%的职工下沉社区帮助困难群众,其中甲单位派出的职工比乙单位少3人。后两单位又在剩下的职工中,分别抽调40%和75%的职工,共计24人参加周末的业务培训。问甲单位职工人数比乙单位:
A少3人
B少11人
C多3人
D多11人
【答案】D
【练习2】某企业参与兴办了甲、乙、丙、丁4个扶贫车间,共投资450万元,甲车间的投资额是其他三个车间投资额之和的一半,乙车间的投资额比丙车间高25%,丁车间的投资额比乙、丙车间投资额之和低60万元。企业后期向4个车间追加了200万元投资,每个车间的追加投资额都不超过其余任一车间追加投资额的2倍,问总投资额最高和最低的车间,总投资额最多可能相差多少万元?
A70
B90
C110
D130
【答案】C










