提到公务员考试的数量关系模块,不少考生都觉得考场上解出一道题目要花费大量时间,得不偿失,但实际上数量关系的题目并不高深,只要我们能够掌握一些基本的方法,许多难题根本不需要太长时间。今天简单介绍一下整除特性方法在一些题目中的简单应用,帮助广大考生备考。
一、定义
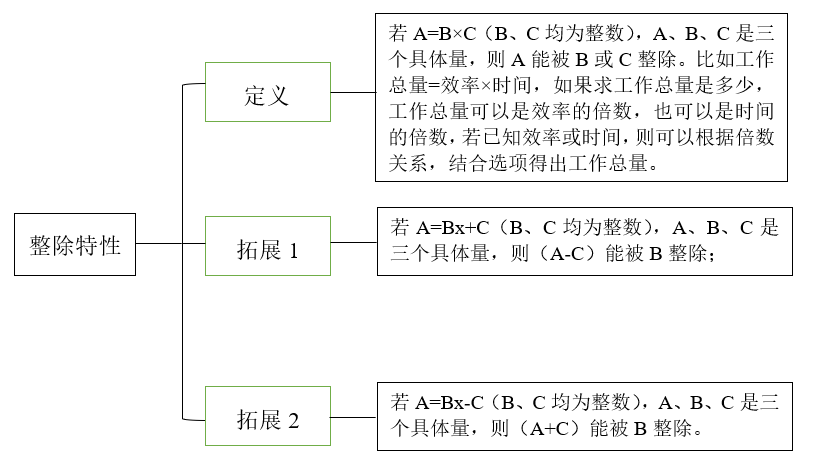
若A=B×C(B、C均为整数),A、B、C是三个具体量,则A能被B或C整除。比如工作总量=效率×时间,如果求工作总量是多少,工作总量可以是效率的倍数,也可以是时间的倍数,若已知效率或时间,则可以根据倍数关系,结合选项得出工作总量。
二、拓展
前面讲的是A=B×C的形式,可以得出A是B、C的倍数;如果考场上所有题目都这样,则题目没有难度,命题人会在此基础上,加减一个数,增加难度。若A=Bx+C,则(A-C)能被B整除;若A=Bx-C,则(A+C)能被B整除。
| 拓展 | 知识点 | ||||||||
| A= | Bx+C | ( | A | -C | ) | 是 | B | 的倍数 | |
| A=Bx-C | ( | A | +C | ) | 是 | B | 的倍数 |
【例1】(2019上海)小李第一次买了A、B、C三种饮料各若干瓶,共花去了75元;之后他再次买了这三种饮料若干瓶,共花去了134元。两次购买的每种饮料数量之和相同,那么若三种饮料各买1瓶最多需花费多少元?(假设饮料价格都是整数元)
A.11
B.15
C.19
D.23

【答案】C
【解析】由题意可知前后两次购买饮料,但买多少瓶未知;本题需要重点理解“两次购买的每种饮料数量之和相同”,设两次购买的每种饮料数量之和均为x瓶,A、B、C饮料的单价是A、B、C,则总花销=价格×瓶数=(A+B+C)×x=75+134=209(元),(A+B+C)×x=209,则(A+B+C)可以被209整除,题目问最多花费多少,因此从最大的选项D代入,209除以23商9余2,排除;再代入选项C,209除以19商11,可整除,因此选择C选项。
【例2】(2019山东)某老旧写字楼重新装修,需要将原有的窗户全部更换为单价90元每扇的新窗户。已知每7扇换下来的旧窗户可以跟厂商兑换一个新窗户。全部更换完毕后共花费16560元且剩余4个旧窗户没有兑换,那么该写字楼一共有多少扇窗户?
A.214
B.218
C.184
D.188
【答案】A
【解析】本题涉及新、旧窗户的兑换,并且给出了窗户的单价和更换完毕后的总花费,已知条件较多。写字楼的窗户分为已经兑换的和没有兑换的,每7扇换下来的旧窗户可以兑换一个新窗户,说明已经兑换的旧窗户是7的倍数,剩余4个旧窗户没有兑换,则旧窗户数量=已经兑换的+4,因此(旧窗户数-4)可以整除7。代入选项验证,A选项214-4=210,是7的倍数,保留;B选项218-4=214,不是7的倍数,排除;C选项184-4=180,不是7的倍数,排除;D选项188-4=184,不是7的倍数,排除;因此选择A选项。
下面总结一下今天学习的思维导图,供大家备考使用。