数字推理公务员考试中都是比较容易得分的部分，然而数字推理中的多次方数列题型多变，特征不明显，总是让人难以识别，无从下手，接下来华图教育带领大家来学习如何从茫茫题海中抓住多次方数列的小尾巴。

　　第一个小尾巴——比较敏感的多次方数

　　多次方数列是由多次方数或由多次方数运算后组成的数列，能够识别多次方数列的关键就是能比较敏感地识别出多次方数。

　　常用多次方数

　　1~21的平方数：1，4，9，16，25，36，49，64，81，100，121，144，169，196，225，256，289，361，400，441

　　1~11的立方数：1，8，27，64，125，216，343，512，729，1000，1331。

　　5的1~5次方：1，25，125，625，3125

　　2的1~10次方：2，4，8，16，32，64，128，256，512，1024

　　多次方数附近的数

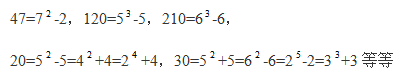
　　例1

　　3，8，15，24，35，( )

　　A.42 B.45 C.48 D.54

　　【分析】24接近5的平方，故本题考虑多次方数列。

　　【答案】C。华图解析：各项依次改写为故本题选C。

　　第二个小尾巴——数列陡增

　　常见的等差数列、和数列、倍数数列中是无法使一个整数突然大幅度变大成为下一项的，故当一个整数数列出现陡增时，可以考虑多次方数列，尝试用前一项的多次方推出后一项，或者前两项的多次方推出后一项。

　　例2

　　2，3，7，45，2017，( )

　　A.4068271 B.4068273

　　C.4068275 D.4068277

　　【分析】题目是单调递增的整数数列，且2017是45的40多倍，数列出现陡增故考虑多次方数列，45接近7的平方，故验证数列是否为平方数列变式。

　　【答案】B。华图解析：平方数列变式，前项的平方减等比数列得到后项。其中减项1、2、4、8、16是公比为2的等比数列。此处可根据尾数确定答案为B。

　　第三个小尾巴——数列中出现和1

　　所有非0整数的0次方是1，所以非0整数的负整数次方是，当数列中同时出现了、1以及其他整数，这个数列很有可能是多次方数列。

　　例3

　　A.1 B.5 C.6 D.8

　　【分析】数列由、1以及其他整数，优先验证是否是多次方数列。

　　【答案】A。华图解析：典型的多次方数列：故本题选A。