在行测试卷中,想必各位小伙伴一听到数量关系,可能就会“头痛”,往往选择放弃,或者是在考试剩下的最后一两分钟,直接进行“蒙题”。不可否认,数量关系中的的确确是有一些比较复杂的题目,而且相较于言语、资料等模块会更容易没有思路,很难短时间内做出。其实只是大家没有正确地认识数量关系,数量关系并不是要求我们必须做到全对,而是只要把其中相对简单的题目做对,尽可能多地将分数拿到手,这样就能够与你的竞争对手形成差距了。

首先,小伙伴们一定要弄清楚数量关系都有哪些知识点,而其中又有哪些知识点是简单的、容易拿分的,或是自己擅长的。所以在大家备考的时候一定要整理好思路,把简单知识点烂熟于心。
![]()
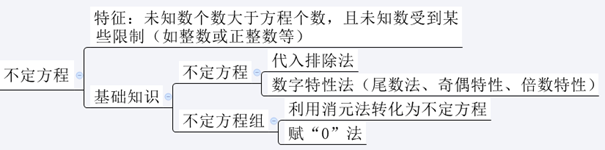
今天小编就给大家分享一个数量关系中简单的知识点:关于不定方程的求解。那么什么叫不定方程呢?大家早在初中、高中时就学习过方程,含有未知数的等式就叫方程。不定方程就是:未知数的个数大于方程的个数,如:,这就是一个不定方程,式子中有两个未知数,但方程只有一个,这就是一个不定方程。那么这个方程如何求解呢?想必小伙伴们心中会有疑惑,与之前的方程不一样,不会解。其实这类方程求解的过程很有技巧性,大家可不要被吓到啊!小编接下来就告诉大家该如何做,因为15是5的倍数,5x也一定是5的倍数,因此,2y也一定是5的倍数,且2y<15,所以y可取值5,解得x为1,这个不定方程就是根据倍数特性进行求解的。除了利用倍数特性,还可以利用代入排除法、奇偶特性、尾数特性等方法求解不等方程。
想必通过这个简单的小例子,小伙伴们对不定方程也有了一定的了解,接下来跟着小编一起做一道真题,再来练习一下。
【例】某次田径运动会中,选手参加各单项比赛计入所在团体总分的规则为:一等奖得9分,二等奖得5分,三等奖得2分。甲队共有10位选手参赛,均获奖。现知甲队最后总分为61分,问该队最多有几位选手获得一等奖?
A. 3 B. 4
C. 5 D. 6
看到这道题,大家最直观的方式就是想利用方程求解,设未知数,列式子来求解。没错,这道题确实可以利用方程来做,我们不妨设甲队获得一等奖、二等奖、三等奖的人数分别为x、y、z,那么就可以根据题干给的信息列出两个等式,9x+5y+2z=61①、x+y+z=10②,所列式子中有3个未知数,只有两个等式,显然这是一个不定方程组。解方程组需要用消元法来做,同样不定方程组也要利用消元法进行消元,想求x可以把y或z消掉。用①-5×②,得到4x-3z=11,接下来就可以通过代入排除法来求解,如果用奇偶特性,只能判断出z是奇数,求不出x。因此,这道题目直接采用代入排除法。问的是最多有几位选手获得一等奖,就要从最大的选项代入,避免代入一个小的选项满足条件就直接选了,然后因为选项并不是满足条件且最大的那个而做错。所以,先代入D选项,解得z不是整数,排除D选项。代入C选项,解得z=3,y=2,C选项符合。因此,选择C选项。
工欲善其事,必先利其器!小伙伴们一定要勤加练习,掌握好知识点。大家一步一个脚印,从简单题开始练习,一定可以学好数量关系的。










