【例 4】 在大小相等的两个等腰直角三角形中 , 按不同的方式各内接一个正方形( 如图 a、b所示) 。如果图 b中的内接正方形的面积是 144 , 那么图 a中的内接正方形
的面积是多少?
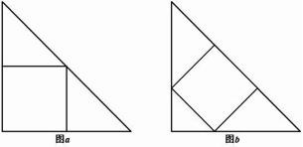
A. 225 B. 162
C. 128 D. 98
【答案】 B
第五章 数量关系
【解析】 第一步 , 本题考查几何问题 , 属于平面几何类 , 用公式法来解题。
第二步, 图 b中正方形的面积是 144 , 故边长为 12 。在等腰直角三 角形 ABC中 ,∠A = ∠C = 45° , 由于 DENM 是正方形 , ∠ADM = ∠CEN = 90° , 故△ADM 与 △CEN 为

全等等腰直角三 角形 , 则 AD = DE = EC , AC = 3DE = 3× 12 = 36 。可得到 BC = 36× =182 。
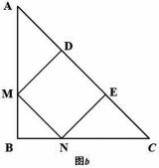

第三步 , 同理 , 图 a正方形的边长为等腰直角三 角形直角边的一半 , 为× 18 2 =92 , 则正方形的面积为 (9 2 ) 2 = 162。
因此, 选择 B选项。
【 拓展】 几何图形比例关系 : 若将一 个图形尺寸扩大为 N倍 , 则 : (1 ) 对应角度 不变 ;(2 ) 对应周长变为原来的 N倍 ; ( 3 ) 面积变为原来的 N2 倍 ; (4 ) 体积变为原来的 N3 倍。
点击添加>>>专属备考微信客服












